MST 알고리즘
1. MST 알고리즘
MST 알고리즘은 그래프에서 모든 정점을 연결하는 간선들의 가중치 합이 최소가 되는 트리를 구성하는 알고리즘이다. MST를 구성하는 방법은 대표적으로 크루스칼과 프림 알고리즘이 있고, 두 알고리즘 모두 각각의 장단점을 가지고 있는 만큼 어느 상황에서 어떤 알고리즘을 사용해야하는지 정리하고자 한다.
모든 정점을 연결하는 트리를 신장 트리라고 부른다. 따라서 신장 트리는 N개의 정점과 N-1개의 간선으로 이루어져 있다.
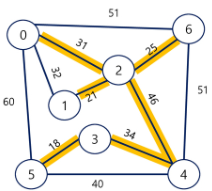
2. 크루스칼 알고리즘
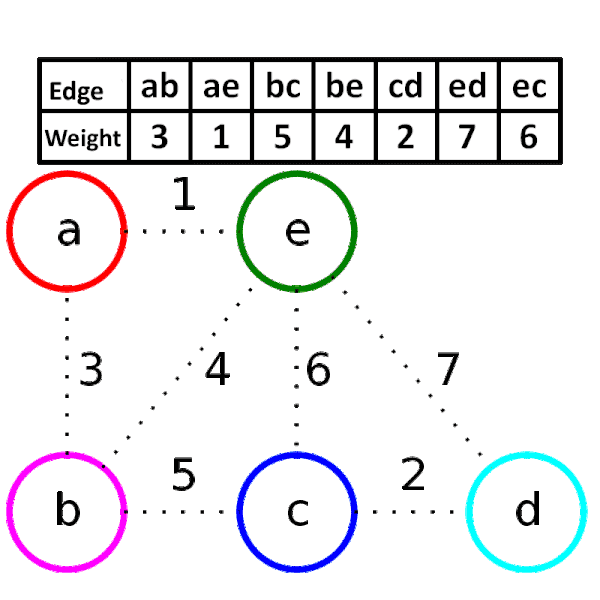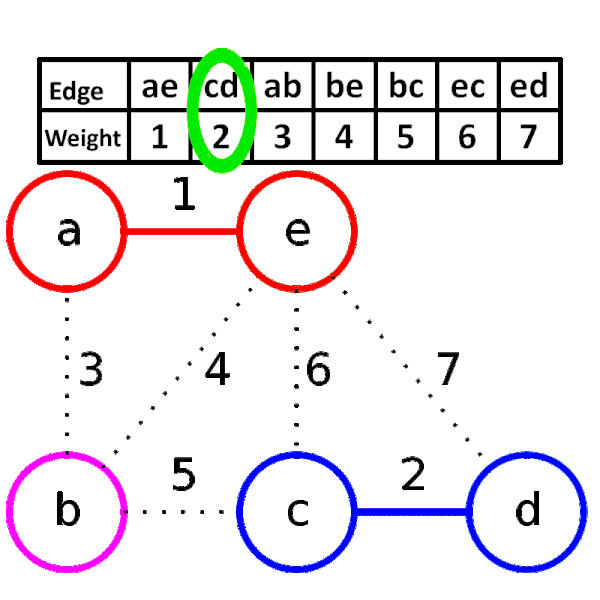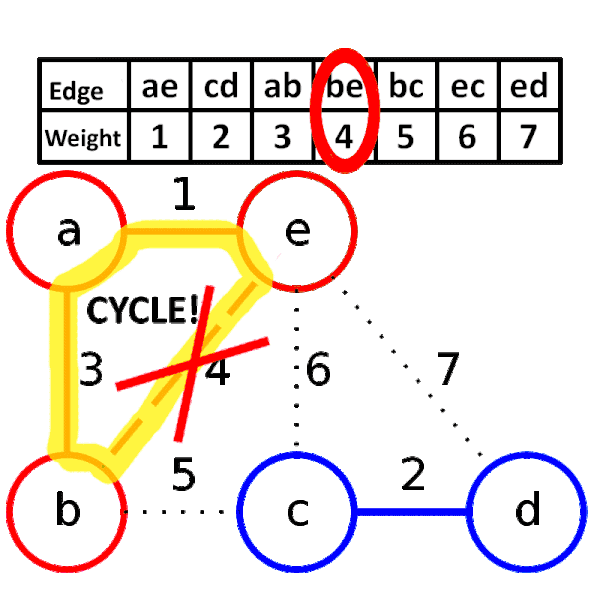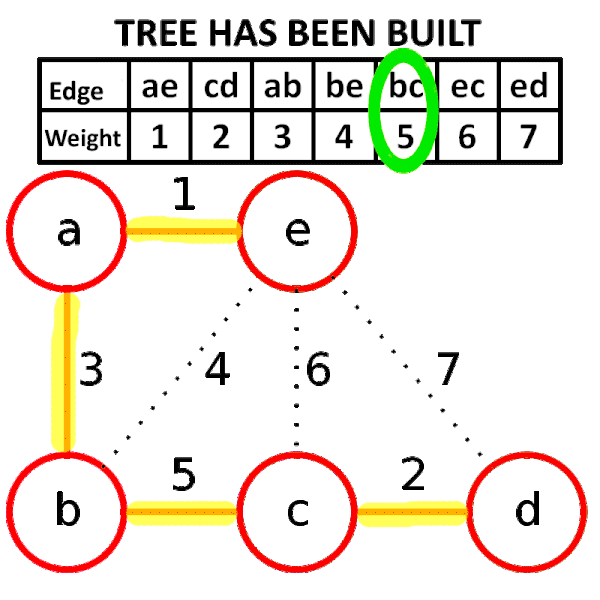
크루스칼 알고리즘은 간선을 기준으로 신장 트리를 구성하는 방법이다. 간선을 기준으로 트리를 구성하기 때문에 간선 개수가 적은 그래프에서 크루스칼 알고리즘을 사용하는 것이 유리하다. 간선을 선택할 때 사이클을 형성하는 것을 방지해야하기 때문에 유니온-파인드를 통해 사이클 여부를 판단하고 신장 트리의 간선을 구성한다.
- 최초 모든 간선을 가중치에 따라 오름차순으로 정렬한다.
- 가중치가 가장 낮은 간선부터 선택하면서 트리를 증가시킨다. 단, 사이클을 형성하는 간선은 선택하지 않는다.
- N-1 개의 간선이 선택될 때까지 위 과정을 반복한다.
소스코드
핵심코드 - O(E log E) : 간선 정렬
// kruskal - 간선 기준 union 연산
int cnt = 0, cost = 0;
for (Edge edge : edgelist) {
// 동일 집합이 아니면 정점 합치기
if (union(edge.start, edge.end)) {
cost += edge.weight;
// 신장 트리 생성 완료
if(++cnt == V-1)
break;
}
}
전체 소스코드(간선 리스트)
import java.io.*;
import java.util.*;
public class MST_KruskalTest {
// 간선 정보
static class Edge implements Comparable<Edge> {
int start, end, weight;
public Edge(int start, int end, int weight) {
this.start = start;
this.end = end;
this.weight = weight;
}
@Override
public int compareTo(Edge o) {
return Integer.compare(this.weight, o.weight);
}
}
static int V, E; // 정점 수, 간선 수
static Edge[] edgelist;
static int[] parents; // 부모원소 관리
/* Disjoint-Set (Union-Find) */
// 모든 원소를 자신을 대표자로 만듦
private static void make() {
parents = new int[V];
for (int i = 0; i < V; i++)
parents[i] = i;
}
// a가 속한 집합의 대표자 찾기
private static int find(int a) {
if (a == parents[a])
return a;
return parents[a] = find(parents[a]); // 최적화 - path compression
}
// 두 원소를 하나의 원소로 합치기 (대표자를 이용해서 합침)
private static boolean union(int a, int b) {
int aRoot = find(a);
int bRoot = find(b);
if (aRoot == bRoot) // 이미 같은 집합
return false;
parents[bRoot] = aRoot; // 대표자끼리 합침
return true;
}
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
V = Integer.parseInt(st.nextToken());
E = Integer.parseInt(st.nextToken());
// 간선리스트 작성
edgelist = new Edge[E];
for (int i = 0; i < E; i++) {
st = new StringTokenizer(br.readLine());
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
int weight = Integer.parseInt(st.nextToken());
edgelist[i] = new Edge(start, end, weight);
}
// 간선 오름차순 정렬
Arrays.sort(edgelist);
// 서로소 집합 생성
make();
// kruskal - 간선 기준 union 연산
int cnt = 0, cost = 0;
for (Edge edge : edgelist) {
// 동일 집합이 아니면 정점 합치기
if (union(edge.start, edge.end)) {
cost += edge.weight;
// 신장 트리 생성 완료
if(++cnt == V-1)
break;
}
}
System.out.println(cost);
}
}
3. 프림 알고리즘
프림 알고리즘은 정점 기준으로 신장 트리를 구성하는 방법이다. 정점을 기준으로 트리를 구성하기 때문에 정점 개수가 적은 그래프에서 프림 알고리즘을 사용하는 것이 유리하다.
프림 알고리즘에서는 다음 정점을 선택할 때는 기존에 선택했던 정점들과 인접하는 정점 중 최소 비용의 간선이 존재하는 정점을 선택한다. 따라서 선택한 정점 집합과 아직 선택되지 않은 정점 집합을 구분하는 로직이 필요하다.
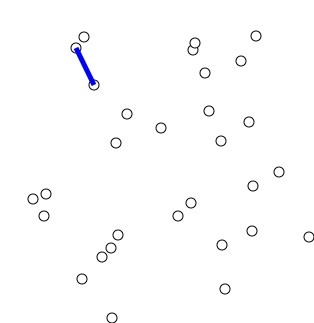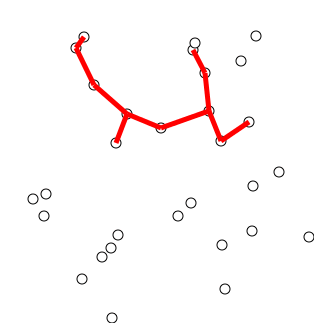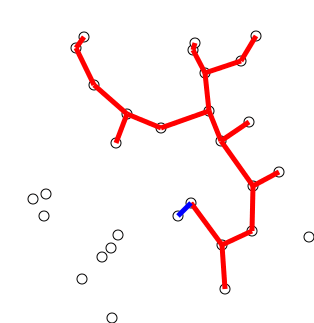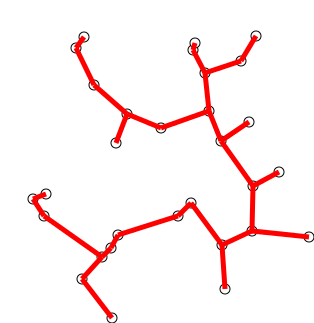
- 임의 정점을 하나 선택해서 시작한다.
- 선택한 정점과 인접하는 정점들 중의 최소 비용의 간선이 존재하는 정점을 선택한다.
- 모든 정점(N)을 선택할 때까지 위 과정을 반복한다.
소스코드
핵심코드 - O(V^2)
int cost = 0;
minEdge[0] = 0; // 시작점 설정
for (int i = 0; i < N; i++) {
// 1. 신장트리에 포함되지 않은 정점 중 최소간선비용 정점 찾기
int min = Integer.MAX_VALUE;
int minVertex = -1;
for (int j = 0; j < N; j++) {
if (!visited[j] && minEdge[j] < min) {
min = minEdge[j];
minVertex = j;
}
}
// 만약 모든 정점이 연결되어있지 않은 경우 (정점이 N개보다 부족한 경우)
// if(minVertex == -1)
// break;
// 2. 신장트리에 선택된 정점 추가, 비용 누적
visited[minVertex] = true;
cost += min;
// 3. 선택된 정점 기준으로 신장트리에 포함되지 않은 정점간 최소 거리 업데이트
for (int j = 0; j < N; j++) {
if(!visited[j] && adjMatrix[minVertex][j] != 0 && minEdge[j] > adjMatrix[minVertex][j]) {
minEdge[j] = adjMatrix[minVertex][j];
}
}
}
전체 소스코드(인접 행렬)
import java.io.*;
import java.util.*;
public class MST_PrimTest {
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine()); // 정점 수
int[][] adjMatrix = new int[N][N]; // 인접 행렬
boolean[] visited = new boolean[N]; // 체크 여부
int[] minEdge = new int[N]; // 정점과의 최소 거리
// 정점 간 거리 정보 저장
for (int i = 0; i < N; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
for (int j = 0; j < N; j++) {
adjMatrix[i][j] = Integer.parseInt(st.nextToken());
}
// 거리 초기화
minEdge[i] = Integer.MAX_VALUE;
}
int cost = 0;
minEdge[0] = 0; // 시작점 설정
for (int i = 0; i < N; i++) {
// 1. 신장트리에 포함되지 않은 정점 중 최소간선비용 정점 찾기
int min = Integer.MAX_VALUE;
int minVertex = -1;
for (int j = 0; j < N; j++) {
if (!visited[j] && minEdge[j] < min) {
min = minEdge[j];
minVertex = j;
}
}
// 2. 신장트리에 선택된 정점 추가, 비용 누적
visited[minVertex] = true;
cost += min;
// 3. 선택된 정점 기준으로 신장트리에 포함되지 않은 정점간 최소 거리 업데이트
for (int j = 0; j < N; j++) {
if(!visited[j] && adjMatrix[minVertex][j] != 0 && minEdge[j] > adjMatrix[minVertex][j]) {
minEdge[j] = adjMatrix[minVertex][j];
}
}
}
}
}
4. 프림 알고리즘(우선순위 큐)
위에서 구현한 프림 알고리즘은 기본적으로 O(V^2) 이지만, 우선순위 큐를 사용하여 최소 거리에 있는 정점을 선택하는 방법으로 최적화할 수 있다. 이렇게 수행할 때의 시간복잡도는 O(V log V + E logV) 이고, 일반적으로 간선의 개수가 정점보다 많으므로 O(E log V) 가 된다.
O(V log V)는 정점에 대한 최소힙 구성을, O(E log V)는 현 정점에서 연결된 간선들(E)을 통해 다음 노드를 확인하는데 그 값이 기존에 저장된 값보다 작으면 다음 정점까지의 거리를 삽입하는 시간이다 (힙 삽입 - log V)
소스코드
핵심코드 - O(E log V)
int cost = 0;
int cnt = 0;
pq.offer(new int[] { 1, 0 }); // 시작 정보
// 다음 탐색할 노드를 우선순위 큐를 통해 판단 - O(E log E) = O(E log V) (E <= V*(V-1)/2)
while (!pq.isEmpty()) {
// 1. 신장트리에 포함되지 않은 정점 중 최소간선비용 정점 찾기
int curr = pq.peek()[0];
int weight = pq.poll()[1];
if (visited[curr])
continue;
// 2. 신장트리에 선택된 정점 추가, 비용 누적
cost += weight;
visited[curr] = true;
// 신장트리 구성 완료
if (cnt++ == V - 1)
break;
// 3. 선택된 정점 기준으로 신장트리에 포함되지 않은 정점간 최소 거리 업데이트
for (Node tmp = nodelist[curr]; tmp != null; tmp = tmp.link) {
if (!visited[tmp.to])
pq.offer(new int[] { tmp.to, tmp.weight });
}
}
전체 소스코드(인접 리스트)
import java.io.*;
import java.util.*;
public class MST_PrimPQTest {
static class Node {
int to, weight;
Node link;
Node(int to, int weight, Node link) {
this.to = to;
this.weight = weight;
this.link = link;
}
}
static int V, E;
static Node[] nodelist;
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
V = Integer.parseInt(st.nextToken());
E = Integer.parseInt(st.nextToken());
// 정점 리스트 입력
nodelist = new Node[V + 1];
for (int i = 0; i < E; i++) {
st = new StringTokenizer(br.readLine());
int from = Integer.parseInt(st.nextToken());
int to = Integer.parseInt(st.nextToken());
int weight = Integer.parseInt(st.nextToken());
nodelist[from] = new Node(to, weight, nodelist[from]);
nodelist[to] = new Node(from, weight, nodelist[to]);
}
boolean[] visited = new boolean[V + 1]; // 방문 여부
PriorityQueue<int[]> pq = new PriorityQueue<>(new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
return Long.compare(o1[1], o2[1]); // weight를 기준으로 정렬
}
}); // 다음 노드 정보 (next Vertex, weight)
int[] minDist = new int[V + 1];
Arrays.fill(minDist, Integer.MAX_VALUE);
long cost = 0;
int cnt = 0;
pq.offer(new int[] { 1, 0 });
// 다음 탐색할 노드를 우선순위 큐를 통해 판단
while (!pq.isEmpty()) {
int curr = pq.peek()[0];
int weight = pq.poll()[1];
if (visited[curr])
continue;
cost += weight;
visited[curr] = true;
if (cnt++ == V - 1)
break;
for (Node tmp = nodelist[curr]; tmp != null; tmp = tmp.link) {
if (!visited[tmp.to])
pq.offer(new int[] { tmp.to, tmp.weight });
}
}
}
}
5. 참고자료
- 크루스칼 알고리즘
- 프림 알고리즘
- 다익스트라 알고리즘 시간복잡도 - O(E log V) 이해용